Օրինակներ երկու մոդուլներով. Թվի մոդուլ (թվի բացարձակ արժեք), սահմանումներ, օրինակներ, հատկություններ
MBOU միջնակարգ դպրոց թիվ 17, Իվանովո
« Հավասարումներ մոդուլով»
Մեթոդական մշակում
Կազմվել է
մաթեմատիկայի ուսուցիչ
Լեբեդևա Ն.Վ.20010 թ
Բացատրական նշում
Գլուխ 1. Ներածություն
Բաժին 2. Հիմնական հատկություններ Բաժին 3. Թվի մոդուլ հասկացության երկրաչափական մեկնաբանությունը Բաժին 4. y = |x| ֆունկցիայի գրաֆիկը Բաժին 5. ԿոնվենցիաներԳլուխ 2. Մոդուլ պարունակող հավասարումների լուծում
Բաժին 1. Ձևի հավասարումներ |F(x)| = m (ամենապարզ) Բաժին 2. F(|x|) = m ձևի հավասարումներ Բաժին 3. Ձևի հավասարումներ |F(x)| = G(x) Բաժին 4. Ձևի հավասարումներ |F(x)| = ± F(x) (ամենագեղեցիկ) Բաժին 5. Ձևի հավասարումներ |F(x)| = |G(x)| Բաժին 6. Ոչ ստանդարտ հավասարումների լուծման օրինակներ Բաժին 7. Ձևի հավասարումներ |F(x)| + |G(x)| = 0 Բաժին 8. Ձևի հավասարումներ |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± n-ում | = մ Բաժին 9. Մի քանի մոդուլներ պարունակող հավասարումներԳլուխ 3. Մոդուլով տարբեր հավասարումների լուծման օրինակներ:
Բաժին 1. Եռանկյունաչափական հավասարումներ Բաժին 2. Էքսպոնենցիալ հավասարումներ Բաժին 3. Լոգարիթմական հավասարումներ Բաժին 4. Իռացիոնալ հավասարումներ Բաժին 5. Ընդլայնված առաջադրանքներ Վարժությունների պատասխաններ ՄատենագիտությունԲացատրական նշում.
Բացարձակ արժեքի հայեցակարգ (մոդուլ) իրական թիվնրա էական հատկանիշներից է։ Այս հայեցակարգը տարածված է ֆիզիկական, մաթեմատիկական և տեխնիկական գիտությունների տարբեր բաժիններում։ Ռուսաստանի Դաշնության ՊՆ ծրագրին համապատասխան միջնակարգ դպրոցներում մաթեմատիկայի դասընթացների դասավանդման պրակտիկայում բազմիցս հանդիպում է «թվի բացարձակ արժեք» հասկացությունը. 6-րդ դասարանում մոդուլի սահմանումը և ներկայացվում է դրա երկրաչափական նշանակությունը. 8-րդ դասարանում ձևավորվում է բացարձակ սխալ հասկացություն, դիտարկվում է մոդուլ պարունակող ամենապարզ հավասարումների և անհավասարությունների լուծումը, ուսումնասիրվում են թվաբանության հատկությունները. քառակուսի արմատ; 11-րդ դասարանում հասկացությունը գտնվում է «Արմատ n-րդ աստիճան»:Դասավանդման փորձը ցույց է տալիս, որ ուսանողները հաճախ դժվարությունների են հանդիպում այս նյութի իմացություն պահանջող առաջադրանքները լուծելիս և հաճախ բաց են թողնում դրանք՝ չսկսելով դրանք ավարտին հասցնել: Նմանատիպ առաջադրանքներ են ներառված նաև 9-րդ և 11-րդ դասարանների քննական առաջադրանքների տեքստերում։ Բացի այդ, այն պահանջները, որոնք բուհերը դնում են դպրոցի շրջանավարտների նկատմամբ, տարբեր են, այն է՝ ավելին բարձր մակարդակքան դպրոցական ուսումնական պլանի պահանջները։ Կյանքի համար ժամանակակից հասարակությունՇատ կարևոր է զարգացնել մաթեմատիկական մտածողության ոճը, որն արտահայտվում է որոշակի մտավոր հմտություններով։ Մոդուլների հետ խնդիրների լուծման գործընթացում պահանջվում է այնպիսի մեթոդներ օգտագործելու ունակություն, ինչպիսիք են ընդհանրացումը և ճշգրտումը, վերլուծությունը, դասակարգումը և համակարգումը և անալոգիան: Նման առաջադրանքների լուծումը թույլ է տալիս ստուգել ձեր գիտելիքները դպրոցական դասընթացի հիմնական բաժինների, մակարդակի վերաբերյալ տրամաբանական մտածողություն, նախնական հետազոտական հմտություններ. այս աշխատանքընվիրված է բաժիններից մեկին՝ մոդուլ պարունակող հավասարումների լուծում։ Այն բաղկացած է երեք գլուխներից. Առաջին գլուխը ներկայացնում է հիմնական հասկացությունները և ամենակարևոր տեսական նկատառումները: Երկրորդ գլխում առաջարկվում են մոդուլ պարունակող հավասարումների ինը հիմնական տեսակներ, քննարկվում են դրանց լուծման մեթոդները և ուսումնասիրվում են օրինակներ տարբեր մակարդակներդժվարություններ. Երրորդ գլխում ներկայացված են ավելի բարդ և ոչ ստանդարտ հավասարումներ (եռանկյունաչափական, էքսպոնենցիալ, լոգարիթմական և իռացիոնալ): Հավասարումների յուրաքանչյուր տեսակի համար կան վարժություններ անկախ որոշում(պատասխանները և հրահանգները կցվում են): Այս աշխատանքի հիմնական նպատակն է ուսուցիչներին մեթոդական աջակցություն ցուցաբերել դասերին նախապատրաստվելու և ընտրովի դասընթացներ կազմակերպելու հարցում: Նյութը կարող է օգտագործվել նաև որպես ուսումնական օգնությունավագ դպրոցի աշակերտների համար. Աշխատանքում առաջարկվող առաջադրանքները հետաքրքիր են և միշտ չէ, որ հեշտ լուծելի են, ինչը հնարավորություն է տալիս ուսանողների կրթական մոտիվացիան ավելի գիտակցված դարձնել, ստուգել նրանց կարողությունները և բարձրացնել դպրոցների շրջանավարտների պատրաստության մակարդակը բուհ ընդունվելու համար: Առաջարկվող վարժությունների տարբերակված ընտրությունը ներառում է նյութի յուրացման վերարտադրողական մակարդակից անցում դեպի ստեղծագործական, ինչպես նաև հնարավորություն սովորեցնելու, թե ինչպես կիրառել ձեր գիտելիքները ոչ ստանդարտ խնդիրներ լուծելիս:Գլուխ 1. Ներածություն.
Բաժին 1. Բացարձակ արժեքի որոշում .
Սահմանում : Իրական թվի բացարձակ արժեքը (մոդուլը): Աոչ բացասական թիվը կոչվում է. Ակամ -Ա. Նշանակում: │ Ա │ Մուտքը հետևյալն է՝ «ա թվի մոդուլ» կամ «ա թվի բացարձակ արժեք».│ ա, եթե a > 0
│a│ = │ 0, եթե a = 0 (1)
│ - և, եթե աՕրինակներ. 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- Ընդլայնել արտահայտման մոդուլը.
Բաժին 2. Հիմնական հատկություններ.
Դիտարկենք բացարձակ արժեքի հիմնական հատկությունները. Գույք թիվ 1: Հակառակ թվերն ունեն հավասար մոդուլներ, այսինքն. │а│=│- а│Եկեք ցույց տանք, որ հավասարությունը ճիշտ է։ Գրենք թվի սահմանումը - Ա : │- ա│= (2) Համեմատենք (1) և (2) բազմությունները։ Ակնհայտ է, որ թվերի բացարձակ արժեքների սահմանումները ԱԵվ - Ահամապատասխանեցնել։ Հետևաբար, │а│=│- а│Հետևյալ հատկությունները դիտարկելիս մենք կսահմանափակվենք դրանց ձևակերպմամբ, քանի որ դրանց ապացույցը բերված է Գույք թիվ 2: Վերջավոր թվով իրական թվերի գումարի բացարձակ արժեքը չի գերազանցում տերմինների բացարձակ արժեքների գումարը՝ │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Գույք թիվ 3: Երկու իրական թվերի տարբերության բացարձակ արժեքը չի գերազանցում դրանց բացարձակ արժեքների գումարը՝ │а - в│ ≤│а│+│в│ Գույք թիվ 4: Վերջավոր թվով իրական թվերի արտադրյալի բացարձակ արժեքը հավասար է գործոնների բացարձակ արժեքների արտադրյալին. │а·в│=│а│·│в│ Գույք թիվ 5: Իրական թվերի քանորդի բացարձակ արժեքը հավասար է դրանց բացարձակ արժեքների քանորդին.
Բաժին 3. Թվի մոդուլ հասկացության երկրաչափական մեկնաբանությունը:
Յուրաքանչյուր իրական թիվ կարող է կապված լինել թվային գծի մի կետի հետ, որը կլինի այս իրական թվի երկրաչափական պատկերը: Թվային տողի յուրաքանչյուր կետ համապատասխանում է սկզբնակետից իր հեռավորությանը, այսինքն. հատվածի երկարությունը սկզբնակետից մինչև տվյալ կետ: Այս հեռավորությունը միշտ համարվում է ոչ բացասական արժեք։ Հետեւաբար, համապատասխան հատվածի երկարությունը կլինի տվյալ իրական թվի բացարձակ արժեքի երկրաչափական մեկնաբանությունը
Ներկայացված երկրաչափական նկարազարդումը հստակ հաստատում է թիվ 1 հատկությունը, այսինքն. մոդուլներ հակադիր թվերհավասար են. Այստեղից հեշտ է հասկանալ հավասարության վավերականությունը՝ │х – а│= │а – x│։ Ավելի ակնհայտ է դառնում նաև │х│= m հավասարման լուծումը, որտեղ m ≥ 0, այն է՝ x 1,2 = ± m: Օրինակներ. 1) │х│= 4 x 1.2 = ± 4 2) │х - 3│= 1
x 1.2 = 2; 4 Բաժին 4. y = │х│ ֆունկցիայի գրաֆիկ
Այս ֆունկցիայի տիրույթը բոլոր իրական թվերն են։Բաժին 5. Կոնվենցիաներ.
Հետագայում հավասարումների լուծման օրինակներ դիտարկելիս կօգտագործվեն հետևյալը խորհրդանիշներ: ( - համակարգի նշան [ - ամբողջության նշան Հավասարումների (անհավասարումների) համակարգը լուծելիս հայտնաբերվում է համակարգում ընդգրկված հավասարումների (անհավասարումների) լուծումների հատումը։ Հավասարումների բազմություն (անհավասարումներ) լուծելիս գտնվում է հավասարումների (անհավասարումների) բազմության մեջ ներառված լուծումների միությունը։Գլուխ 2. Մոդուլ պարունակող հավասարումների լուծում:
Այս գլխում մենք կանդրադառնանք մեկ կամ մի քանի մոդուլ պարունակող հավասարումների լուծման հանրահաշվական մեթոդներին:Բաժին 1. │F (x)│= m ձևի հավասարումներ
Այս տեսակի հավասարումը կոչվում է ամենապարզը: Այն լուծում ունի, եթե և միայն, եթե m ≥ 0: Ըստ մոդուլի սահմանման, սկզբնական հավասարումը համարժեք է երկու հավասարումների բազմությանը. │ Ֆ(x)│=մ
Օրինակներ.
№1. Լուծե՛ք հավասարումը` │7х - 2│= 9
Պատասխան՝ x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│ = 1
x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Պատասխան՝ արմատների գումարը 2 է.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 նշանակում x 2 = m, m ≥ 0 x = 0 ; ±√5 մ 2 – 5 մ + 4 = 0 մ = 1; 4 – երկու արժեքներն էլ բավարարում են պայմանը m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Պատասխան՝ 7-րդ հավասարման արմատների թիվը։ Վարժություններ:
№1. Լուծե՛ք հավասարումը և նշե՛ք արմատների գումարը՝ │х - 5│= 3 №2 . Լուծե՛ք հավասարումը և նշե՛ք ավելի փոքր արմատը՝ │x 2 + x│= 0 №3 . Լուծե՛ք հավասարումը և նշե՛ք ավելի մեծ արմատ│x 2 – 5x + 4│= 4 №4 .Լուծե՛ք հավասարումը և նշե՛ք ամբողջ արմատը՝ │2x 2 – 7x + 6│= 1 №5 .Լուծե՛ք հավասարումը և նշե՛ք արմատների թիվը՝ │x 4 – 13x 2 + 50│= 14.
Բաժին 2. F(│х│) = m ձևի հավասարումներ
Ձախ կողմում ֆունկցիայի փաստարկը գտնվում է մոդուլի նշանի տակ, իսկ աջ կողմը անկախ է փոփոխականից: Դիտարկենք այս տիպի հավասարումների լուծման երկու եղանակ: 1 ճանապարհ:Բացարձակ արժեքի սահմանմամբ սկզբնական հավասարումը համարժեք է երկու համակարգերի համակցությանը։ Որոնցից յուրաքանչյուրում պայման է դրվում ենթամոդուլային արտահայտության վրա։ Ֆ(│х│) =մ
Քանի որ F(│x│) ֆունկցիան հավասար է սահմանման ողջ տիրույթում, F(x) = m և F(- x) = m հավասարումների արմատները հակադիր թվերի զույգեր են: Ուստի բավական է լուծել համակարգերից մեկը (այսպես օրինակներ դիտարկելիս կտրվի մեկ համակարգի լուծումը)։ Մեթոդ 2:Նոր փոփոխականի ներդրման մեթոդի կիրառում. Այս դեպքում ներմուծվում է │x│= a նշումը, որտեղ a ≥ 0: Այս մեթոդըդիզայնով ավելի քիչ ծավալուն: Օրինակներ. №1 . Լուծեք հավասարումը. 3x 2 – 4│x│= - 1 Եկեք օգտագործենք նոր փոփոխականի ներդրումը: Նշենք │x│= a, որտեղ a ≥ 0: Ստանում ենք 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 հավասարումը. Վերադառնալ սկզբնական փոփոխականին՝ │ x│=1 և │х│= 1/3: Յուրաքանչյուր հավասարում ունի երկու արմատ: Պատասխան՝ x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Լուծե՛ք հավասարումը. 5x 2 + 3│x│- 1 = 1/2 │x│ + 3x 2
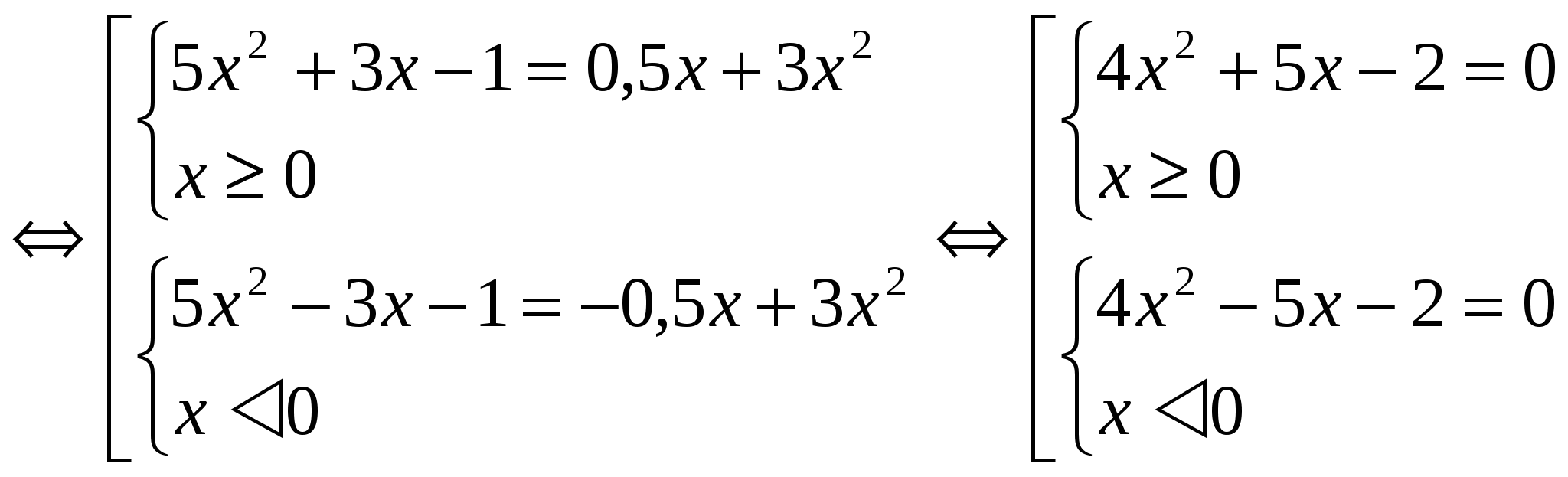Եկեք գտնենք բնակչության առաջին համակարգի լուծումը՝ 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Նկատի ունեցեք, որ x 2-ը չի բավարարում. պայմանը x ≥ 0. Լուծում երկրորդ համակարգը կլինի x 1 արժեքին հակառակ թիվը: Պատասխան՝ x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Լուծե՛ք հավասարումը` x 4 – │х│= 0 Նշենք │х│= a, որտեղ a ≥ 0: Ստացվում է a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 հավասարումը. a 2 = 1 Վերադառնալ սկզբնական փոփոխականին՝ │х│=0 և │х│= 1 x = 0; ± 1 Պատասխան՝ x 1
= 0; X 2
= 1; X 3
= - 1.
Վարժություններ: №6. Լուծեք հավասարումը. 2│х│ - 4.5 = 5 – 3 / 8 │х│ №7 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների քանակը՝ 3x 2 - 7│x│ + 2 = 0 №8 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք ամբողջական լուծումներ՝ x 4 + │x│ - 2 = 0
Բաժին 3. │F(x)│ = G(x) ձևի հավասարումներ.
Այս տիպի հավասարման աջ կողմը կախված է փոփոխականից և, հետևաբար, ունի լուծում, եթե և միայն այն դեպքում, եթե աջ կողմը G(x) ≥ 0 ֆունկցիա է: Սկզբնական հավասարումը կարող է լուծվել երկու եղանակով: : 1 ճանապարհ:Ստանդարտ, որը հիմնված է մոդուլի բացահայտման վրա՝ հիմնված դրա սահմանման վրա և բաղկացած է համարժեք անցումից երկու համակարգերի համակցությանը: │ Ֆ(x)│ =Գ(X)
Այս մեթոդը կարող է ռացիոնալ կերպով օգտագործվել G(x) ֆունկցիայի բարդ արտահայտության դեպքում, իսկ F(x) ֆունկցիայի համար ավելի քիչ բարդ արտահայտության դեպքում, քանի որ ենթադրվում է, որ F(x) ֆունկցիայի անհավասարությունները կլուծվեն: Մեթոդ 2:Բաղկացած է համարժեք համակարգի անցումից, որտեղ պայման է դրվում աջ կողմում: │ Ֆ(x)│=
Գ(x)
Այս մեթոդը ավելի հարմար է օգտագործել, եթե G(x) ֆունկցիայի արտահայտությունն ավելի քիչ բարդ է, քան F(x) ֆունկցիայի համար, քանի որ ենթադրվում է նաև G(x) ≥ 0 անհավասարության լուծումը մի քանի մոդուլներից, խորհուրդ է տրվում օգտագործել երկրորդ տարբերակը: Օրինակներ.
№1.
Լուծե՛ք հավասարումը` │x + 2│= 6 -2x 
(1 ճանապարհ) Պատասխան՝ x = 1 1
/
3
№2.
│х 2 – 2х - 1│= 2·(x + 1)
(2 ճանապարհ) Պատասխան՝ Արմատների արտադրյալը 3 է։№3. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը.
│x - 6│= x 2 - 5x + 9
Պատասխան՝ արմատների գումարը 4 է։
Վարժություններ: №9. │x + 4│= - 3x №10. Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք լուծումների քանակը՝│x 2 + x - 1│= 2x – 1 №11 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների արտադրյալը՝│x + 3│= x 2 + x – 6
Բաժին 4. │F(x)│= F(x) և │F(x)│= - F(x) ձևի հավասարումներ.
Այս տեսակի հավասարումները երբեմն անվանում են «ամենագեղեցիկ»։ Քանի որ հավասարումների աջ կողմը կախված է փոփոխականից, լուծումներ կան, եթե և միայն այն դեպքում, երբ աջ կողմը ոչ բացասական է: Հետևաբար, սկզբնական հավասարումները համարժեք են անհավասարություններին.│F(x)│= F(x) F(x) ≥ 0 և │F(x)│= - F(x) F(x) Օրինակներ. №1 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք ավելի փոքր ամբողջական արմատը՝ │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 Պատասխան՝ x = 1№2. Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք միջակայքի երկարությունը՝ │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Պատասխան՝ միջակայքի երկարությունը 6 է։№3 . Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամբողջ թվային լուծումների քանակը՝ │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Պատասխան՝ 4 ամբողջական լուծում։№4 . Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամենամեծ արմատը.
│4 – x -
│= 4 – x – 
x 2 – 5x + 5 = 0 D = 5 x 1.2 = 
≈ 1,4Պատասխան՝ x = 3:
Վարժություններ:
№12.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ամբողջ արմատը՝ │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք ամբողջ թվային լուծումների քանակը՝ │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
Լուծեք հավասարումը ձեր պատասխանում, նշեք մի ամբողջ թիվ, որը հավասարման արմատը չէ. 
Բաժին 5. │F(x)│= │G(x)│ ձևի հավասարումներ.
Քանի որ հավասարման երկու կողմերն էլ ոչ բացասական են, լուծումը ներառում է երկու դեպք՝ ենթամոդուլային արտահայտությունները հավասար են կամ հակառակ նշանով: Հետևաբար, սկզբնական հավասարումը համարժեք է երկու հավասարումների համակցությանը՝ │ Ֆ(x)│= │ Գ(x)│
Օրինակներ.
№1.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ամբողջ արմատը՝ │x + 3│=│2x - 1│ 
Պատասխան՝ ամբողջ արմատ x = 4:№2.
Լուծե՛ք հավասարումը. │
x – x 2 - 1│=│2x – 3 – x 2 │ 
Պատասխան՝ x = 2:№3
.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների արտադրյալը. 
Արմատային հավասարումներ 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 Պատասխան՝ արմատների արտադրյալը 0,25 է: Վարժություններ:
№15
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամբողջ լուծումը՝ │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ավելի փոքր արմատը՝│5x - 3│=│7 - x│ №17
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. 
Բաժին 6. Ոչ ստանդարտ հավասարումների լուծման օրինակներ
Այս բաժնում մենք կանդրադառնանք ոչ ստանդարտ հավասարումների օրինակներին, որոնք լուծելիս արտահայտության բացարձակ արժեքը բացահայտվում է ըստ սահմանման: Օրինակներ.№1.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ x · │x│- 5x – 6 = 0 
Պատասխան՝ արմատների գումարը 1 է №2.
.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ավելի փոքր արմատը՝ x 2 - 4x · 
- 5 = 0 
Պատասխան՝ ավելի փոքր արմատ x = - 5: №3.
Լուծե՛ք հավասարումը. 
Պատասխան՝ x = -1: Վարժություններ:
№18.
Լուծե՛ք հավասարումը և նշե՛ք արմատների գումարը՝ x · │3x + 5│= 3x 2 + 4x + 3
№19.
Լուծե՛ք հավասարումը x 2 – 3x = 
№20.
Լուծե՛ք հավասարումը. 
Բաժին 7. │F(x)│+│G(x)│=0 ձևի հավասարումներ.
Հեշտ է նկատել, որ այս տիպի հավասարման ձախ կողմում ոչ բացասական մեծությունների գումարն է։ Հետևաբար, սկզբնական հավասարումը լուծում ունի, եթե և միայն այն դեպքում, եթե երկու անդամները միաժամանակ հավասար են զրոյի: Հավասարումը համարժեք է հավասարումների համակարգին՝ │ Ֆ(x)│+│ Գ(x)│=0
Օրինակներ.
№1
. Լուծե՛ք հավասարումը. 
Պատասխան՝ x = 2: №2.
Լուծե՛ք հավասարումը. Պատասխան՝ x = 1: Վարժություններ:
№21.
Լուծե՛ք հավասարումը. №22
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. №23
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք լուծումների քանակը. Բաժին 8. │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m ձևի հավասարումներ
Այս տեսակի հավասարումները լուծելու համար օգտագործվում է ինտերվալ մեթոդը: Եթե այն լուծենք մոդուլների հաջորդական ընդլայնմամբ, կստանանք nհամակարգերի հավաքածուներ, ինչը շատ դժվար է և անհարմար: Դիտարկենք ինտերվալ մեթոդի ալգորիթմը՝ 1). Գտեք փոփոխական արժեքներ X, որի համար յուրաքանչյուր մոդուլ հավասար է զրոյի (ենթամոդուլային արտահայտությունների զրո).
2). Նշեք գտնված արժեքները թվային տողի վրա, որը բաժանված է միջակայքերի (ինտերվալների թիվը համապատասխանաբար հավասար է. n+1
) 3). Որոշեք, թե յուրաքանչյուր մոդուլ ինչ նշանով է բացահայտվում ստացված յուրաքանչյուր միջակայքում (լուծում կատարելիս կարող եք օգտագործել թվային տող՝ նշելով դրա վրա նշանները) 4): Սկզբնական հավասարումը համարժեք է ագրեգատին n+1
համակարգեր, որոնցից յուրաքանչյուրում նշվում է փոփոխականի անդամակցությունը Xընդմիջումներից մեկը. Օրինակներ.
№1
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամենամեծ արմատը. 
1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 2; x = -3 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլ ստացված միջակայքերի վրա. x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- լուծումներ չկան Հավասարումն ունի երկու արմատ: Պատասխան՝ ամենամեծ արմատը x = 2: №2.
Լուծե՛ք հավասարումը և ձեր պատասխանում տրամադրե՛ք ամբողջ արմատը. 
1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 1,5; x = - 1 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե յուրաքանչյուր մոդուլ ինչ նշանով է բացահայտվում ստացված միջակայքերի վրա՝ x + 1 x + 1 x + 1 - + + -1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Վերջին համակարգը լուծումներ չունի, հետևաբար հավասարումն ունի երկու արմատ։ Հավասարումը լուծելիս պետք է ուշադրություն դարձնել երկրորդ մոդուլի դիմաց գտնվող «-» նշանին։ Պատասխան՝ ամբողջ արմատ x = 7: №3.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ 1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 5; x = 1; x = - 2 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլ ստացված միջակայքում՝ x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Հավասարումն ունի երկու արմատ x = 0 և 2: Պատասխան՝ արմատների գումարը 2 է։ №4
.
Լուծե՛ք հավասարումը. 1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 1; x = 2; x = 3. 2): Եկեք որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլը ստացված միջակայքերի վրա։ 3). 
Եկեք համատեղենք առաջին երեք համակարգերի լուծումները: Պատասխան՝ ; x = 5.Վարժություններ: №24. Լուծե՛ք հավասարումը.
№25.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. №26.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ավելի փոքր արմատը. №27.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ավելի մեծ արմատը. Բաժին 9. Մի քանի մոդուլներ պարունակող հավասարումներ
Բազմաթիվ մոդուլներ պարունակող հավասարումները ենթադրում են բացարձակ արժեքների առկայություն ենթամոդուլային արտահայտություններում: Այս տեսակի հավասարումների լուծման հիմնական սկզբունքը մոդուլների հաջորդական բացահայտումն է՝ սկսած «արտաքինից»: Լուծման ժամանակ օգտագործվում են թիվ 1, թիվ 3 բաժիններում քննարկված տեխնիկան։Օրինակներ.
№1.
Լուծե՛ք հավասարումը. 
Պատասխան՝ x = 1; - տասնմեկ: №2.
Լուծե՛ք հավասարումը.
Պատասխան՝ x = 0; 4; - 4. №3.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների արտադրյալը. 
Պատասխան՝ արմատների արտադրյալը 8 է։ №4.
Լուծե՛ք հավասարումը. 
Նշենք բնակչության հավասարումները (1)
Եվ (2)
և դիզայնի հեշտության համար հաշվի առեք դրանցից յուրաքանչյուրի լուծումը առանձին: Քանի որ երկու հավասարումներն էլ պարունակում են մեկից ավելի մոդուլ, ավելի հարմար է համարժեք անցում կատարել համակարգերի հավաքածուներին: (1)
(2)
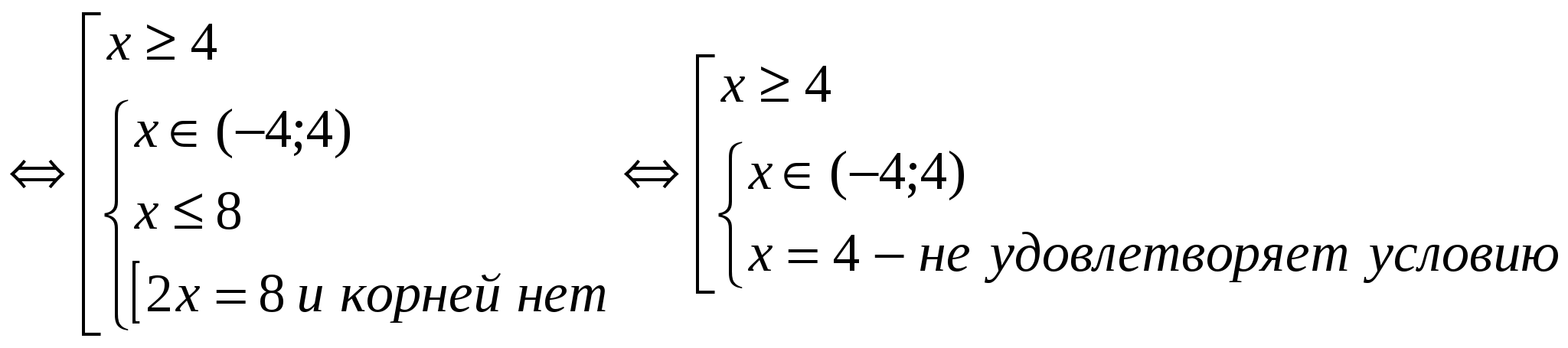Պատասխան.
Վարժություններ:
№36.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ 5 │3x-5│ = 25 x №37.
Լուծե՛ք հավասարումը, եթե կա մեկից ավելի արմատ, ապա ձեր պատասխանում նշե՛ք արմատների գումարը՝ │x + 2│ x – 3x – 10 = 1 №38.
Լուծե՛ք հավասարումը. 3 │2x -4│ = 9 │x│ №39.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների թիվը՝ 2 │ sin x│ = √2 №40
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների թիվը.
Բաժին 3. Լոգարիթմական հավասարումներ.
Հետևյալ հավասարումները լուծելուց առաջ անհրաժեշտ է վերանայել լոգարիթմների հատկությունները և լոգարիթմական ֆունկցիան։ Օրինակներ. №1. Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների արտադրյալը՝ log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1Դեպք 1. եթե x ≥ - 1, ապա log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – բավարարում է x ≥ - 1 2 պայմանը. եթե x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – բավարարում է x - 1 պայմանը
Պատասխան՝ արմատների արտադրյալը 15 է։
№2.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ lg 
Օ.Դ.Զ. 
Պատասխան՝ արմատների գումարը 0,5 է։
№3.
Լուծե՛ք հավասարումը log 5 
Օ.Դ.Զ. 
Պատասխան՝ x = 9: №4.
Լուծե՛ք հավասարումը` │2 + լոգ 0,2 x│+ 3 = │1 + լոգ 5 x│ O.D.Z. x > 0 Եկեք օգտագործենք մեկ այլ հիմք տեղափոխելու բանաձևը: │2 - մատյան 5 x│+ 3 = │1 + մատյան 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 25; x = Այս թվերը բաժանում են տարածքը ընդունելի արժեքներերեք ընդմիջումներով, ուստի հավասարումը համարժեք է երեք համակարգերի բազմությանը: 
Պատասխանեք:)
