Property of opposite sides of a parallelogram. Calculate the sum of angles and area of a parallelogram: properties and characteristics
QUADAGONS.
§43. PARALLELOGRAM.
1. Definition of a parallelogram.
If we intersect a pair of parallel lines with another pair of parallel lines, we get a quadrilateral whose opposite sides are parallel in pairs.
In quadrilaterals ABC and EFNM (Fig. 224) ВD || AC and AB || CD;
EF || MN and EM || FN.
A quadrilateral whose opposite sides are parallel in pairs is called a parallelogram.
2. Properties of a parallelogram.
Theorem. The diagonal of a parallelogram divides it into two equal triangles.
Let there be a parallelogram ABC (Fig. 225), in which AB || CD and AC || ВD.
You need to prove that the diagonal divides it into two equal triangles.
Let us draw diagonal CB in parallelogram ABC. Let's prove that /\ CAB= /\ C.D.B.
The NE side is common to these triangles; / ABC = / BCD, as internal crosswise angles with parallel AB and CD and secant CB; / DIA = / СВD, also like internal crosswise angles with parallel AC and ВD and secant CB (§ 38).

From here /\ CAB = /\ C.D.B.
In the same way, one can prove that the diagonal AD will divide the parallelogram into two equal triangles ACD and ABD.
Consequences. 1 . Opposite angles of a parallelogram are equal to each other.
/
A = /
D, this follows from the equality of triangles CAB and CDB.
Likewise /
C = /
IN.
2. The opposite sides of a parallelogram are equal to each other.
AB = CD and AC = BD, since these are sides of equal triangles and lie opposite equal angles.
Theorem 2. The diagonals of a parallelogram are divided in half at the point of their intersection.
Let BC and AD be the diagonals of the parallelogram ABC (Fig. 226). Let us prove that AO = OD and CO = OB.
To do this, compare some pair of opposite triangles, for example /\ AOB and /\ COD.
In these triangles AB = CD, like opposite sides of a parallelogram;
/
1 = /
2, as interior angles lying crosswise with parallel AB and CD and secant AD;
/
3 = /
4 for the same reason, since AB || CD and CB are their secant (§ 38).
It follows that /\ AOB = /\ COD. And in equal triangles, equal sides lie opposite equal angles. Therefore, AO = OD and CO = OB.
Theorem 3. The sum of the angles adjacent to one side of a parallelogram is equal to 2 d .
Prove it yourself.
3. Signs of a parallelogram.
Theorem. If the opposite sides of a quadrilateral are equal in pairs, then this quadrilateral is a parallelogram.
Let in the quadrilateral ABC (Drawn 227) AB = CD and AC = BD. Let us prove that under this condition AB || CD and AC || ВD, i.e. quadrilateral АВDC is a parallelogram.
Let us connect with a segment any two opposite vertices of this quadrilateral, for example C and B. The quadrilateral ABC is divided into two equal triangles: /\
CAB and /\
C.D.B. In fact, they have the same side CB, AB = CD and AC = BD according to the condition. Thus, three sides of one triangle are respectively equal to three sides of another, therefore /\
CAB = /\
C.D.B.

In equal triangles against equal sides the angles are equal, so
/
1 = /
2 and /
3 = /
4.
Angles 1 and 2 are internal angles lying crosswise at the intersection of straight lines AB and CD of straight line CB. Therefore, AB || CD.
In the same way, angles 3 and 4 are internal angles lying crosswise at the intersection of lines CA and BD of line CB, therefore, CA || ВD (§ 35).
Thus, the opposite sides of the quadrilateral ABC are parallel in pairs, therefore, it is a parallelogram, which is what needed to be proven.
Theorem 2. If two opposite sides of a quadrilateral are equal and parallel, then the quadrilateral is a parallelogram.
Let in the quadrilateral ABCD AB = CD and AB || CD. Let us prove that under these conditions the quadrilateral ABC is a parallelogram (Fig. 228).

Let us connect vertices C and B with a segment CB. Due to the parallelism of straight lines AB and CD, angles 1 and 2, as internal angles lying crosswise, are equal (§ 38).
Then triangle CAB is equal to triangle CDB, since they have a common side CB,
AB = CD according to the theorem and /
1 = /
2 according to proven. The equality of these triangles implies the equality of angles 3 and 4, since they lie opposite equal sides in equal triangles.
But angles 3 and 4 are internal crosswise angles formed by the intersection of straight lines AC and BD of straight line CB, therefore, AC || ВD (§ 35), i.e. a quadrilateral
ABC is a parallelogram.
Exercises.
1. Prove that if the diagonals of a quadrilateral at the point of their mutual intersection are divided in half, then this quadrilateral is a parallelogram.
2. Prove that a quadrilateral whose sum internal corners adjacent to each of two adjacent sides is equal to 2 d, there is a parallelogram.
3. Construct a parallelogram using two sides and the angle between them:
a) using the parallelism of opposite sides of a parallelogram;
b) using the equality of opposite sides of a parallelogram.
4. Construct a parallelogram using two adjacent sides and a diagonal.
5. Construct a parallelogram using its two diagonals and the angle between them.
6. Construct a parallelogram using its side and two diagonals.
Average level
Parallelogram, rectangle, rhombus, square (2019)
1. Parallelogram
Compound word "parallelogram"? And behind it lies a very simple figure.
Well, that is, we took two parallel lines:

Crossed by two more:

And inside there is a parallelogram!
What properties does a parallelogram have?
Properties of a parallelogram.
That is, what can you use if a parallelogram is given in the problem?
The following theorem answers this question:
Let's draw everything in detail.
What does it mean first point of the theorem? And the fact is that if you HAVE a parallelogram, then you will certainly
The second point means that if there IS a parallelogram, then, again, certainly:
Well, and finally, the third point means that if you HAVE a parallelogram, then be sure to:
Do you see what a wealth of choice there is? What to use in the problem? Try to focus on the question of the task, or just try everything one by one - some “key” will do.
Now let’s ask ourselves another question: how can we recognize a parallelogram “by sight”? What must happen to a quadrilateral so that we have the right to give it the “title” of a parallelogram?
Several signs of a parallelogram answer this question.
Signs of a parallelogram.
Attention! Begin.
Parallelogram.
Please note: if you found at least one sign in your problem, then you definitely have a parallelogram, and you can use all the properties of a parallelogram.
2. Rectangle
I think that it will not be news to you at all that
First question: is a rectangle a parallelogram?
Of course it is! After all, he has - remember, our sign 3?
And from here, of course, it follows that in a rectangle, like in any parallelogram, the diagonals are divided in half by the point of intersection.
But the rectangle also has one distinctive property.
Rectangle property
Why is this property distinctive? Because no other parallelogram has equal diagonals. Let's formulate it more clearly.
Please note: in order to become a rectangle, the quadrilateral must first become a parallelogram, and then show the equality of the diagonals.
3. Diamond
And again the question: is a rhombus a parallelogram or not?
With full right - a parallelogram, because it has and (remember our feature 2).
And again, since a rhombus is a parallelogram, then it must have all the properties of a parallelogram. This means that the rhombus opposite angles are equal, opposite sides are parallel, and the diagonals are bisected by the point of intersection.
Properties of a rhombus
Look at the picture:

As in the case of a rectangle, these properties are distinctive, that is, for each of these properties we can conclude that this is not just a parallelogram, but a rhombus.
Signs of a diamond


And again, pay attention: there must be not just a quadrilateral whose diagonals are perpendicular, but a parallelogram. Make sure:
No, of course, although its diagonals are perpendicular, and the diagonal is the bisector of the angles and. But... diagonals are not divided in half by the point of intersection, therefore - NOT a parallelogram, and therefore NOT a rhombus.
That is, a square is a rectangle and a rhombus at the same time. Let's see what happens.
Is it clear why? - rhombus is the bisector of angle A, which is equal to. This means it divides (and also) into two angles along.
Well, it's quite clear: the diagonals of a rectangle are equal; The diagonals of a rhombus are perpendicular, and in general, a parallelogram of diagonals is divided in half by the point of intersection.
AVERAGE LEVEL
Properties of quadrilaterals. Parallelogram

Properties of a parallelogram
Attention! Words " properties of a parallelogram"mean that if in your task There is parallelogram, then all of the following can be used.
Theorem on the properties of a parallelogram.
In any parallelogram:
Let's understand why this is all true, in other words WE'LL PROVE theorem.
So why is 1) true?
If it is a parallelogram, then:
- lying like criss-cross
- lying like crosses.
This means (according to criterion II: and - general.)
Well, that’s it, that’s it! - proved.
But by the way! We also proved 2)!
Why? But (look at the picture), that is, precisely because.
Only 3 left).
To do this, you still have to draw a second diagonal.
And now we see that - according to the II characteristic (angles and the side “between” them).
Properties proven! Let's move on to the signs.
Signs of a parallelogram
Recall that the parallelogram sign answers the question “how do you know?” that a figure is a parallelogram.
In icons it's like this:
Why? It would be nice to understand why - that's enough. But look:
Well, we figured out why sign 1 is true.
Well, it's even easier! Let's draw a diagonal again.
Which means:
AND It's also easy. But...different!
Means, . Wow! But also - internal one-sided with a secant!
Therefore the fact that means that.
And if you look from the other side, then - internal one-sided with a secant! And therefore.
Do you see how great it is?!
And again simple:
Exactly the same, and.
Pay attention: if you found at least one sign of a parallelogram in your problem, then you have exactly parallelogram and you can use everyone properties of a parallelogram.
For complete clarity, look at the diagram:

Properties of quadrilaterals. Rectangle.
Rectangle properties:
Point 1) is quite obvious - after all, sign 3 () is simply fulfilled
And point 2) - very important. So, let's prove that
This means on two sides (and - general).
Well, since the triangles are equal, then their hypotenuses are also equal.
Proved that!
And imagine, equality of diagonals is a distinctive property of a rectangle among all parallelograms. That is, this statement is true^
Let's understand why?
This means (meaning the angles of a parallelogram). But let us remember once again that it is a parallelogram, and therefore.
Means, . Well, of course, it follows that each of them! After all, they have to give in total!
So they proved that if parallelogram suddenly (!) the diagonals turn out to be equal, then this exactly a rectangle.
But! Pay attention! This is about parallelograms! Not just anyone a quadrilateral with equal diagonals is a rectangle, and only parallelogram!
Properties of quadrilaterals. Rhombus
And again the question: is a rhombus a parallelogram or not?
With full right - a parallelogram, because it has (Remember our feature 2).
And again, since a rhombus is a parallelogram, it must have all the properties of a parallelogram. This means that in a rhombus, opposite angles are equal, opposite sides are parallel, and the diagonals bisect at the point of intersection.
But there are also special properties. Let's formulate it.
Properties of a rhombus
Why? Well, since a rhombus is a parallelogram, then its diagonals are divided in half.
Why? Yes, that's why!
In other words, the diagonals turned out to be bisectors of the corners of the rhombus.
As in the case of a rectangle, these properties are distinctive, each of them is also a sign of a rhombus.
Signs of a diamond.
Why is this? And look,
That means both These triangles are isosceles.
To be a rhombus, a quadrilateral must first “become” a parallelogram, and then exhibit feature 1 or feature 2.
Properties of quadrilaterals. Square
That is, a square is a rectangle and a rhombus at the same time. Let's see what happens.
Is it clear why? A square - a rhombus - is the bisector of an angle that is equal to. This means it divides (and also) into two angles along.
Well, it's quite clear: the diagonals of a rectangle are equal; The diagonals of a rhombus are perpendicular, and in general, a parallelogram of diagonals is divided in half by the point of intersection.
Why? Well, let's just apply the Pythagorean theorem to...
SUMMARY AND BASIC FORMULAS
Properties of a parallelogram:
- Opposite sides are equal: , .
- Opposite angles are equal: , .
- The angles on one side add up to: , .
- The diagonals are divided in half by the intersection point: .
Rectangle properties:
- The diagonals of the rectangle are equal: .
- A rectangle is a parallelogram (for a rectangle all the properties of a parallelogram are fulfilled).
Properties of a rhombus:
- The diagonals of a rhombus are perpendicular: .
- The diagonals of a rhombus are the bisectors of its angles: ; ; ; .
- A rhombus is a parallelogram (for a rhombus all the properties of a parallelogram are fulfilled).
Properties of a square:
A square is a rhombus and a rectangle at the same time, therefore, for a square all the properties of a rectangle and a rhombus are fulfilled. And.
Problem 1. One of the angles of the parallelogram is 65°. Find the remaining angles of the parallelogram.
∠C =∠A = 65° as opposite angles of a parallelogram.
∠A +∠B = 180° as angles adjacent to one side of a parallelogram.
∠B = 180° - ∠A = 180° - 65° = 115°.
∠D =∠B = 115° as the opposite angles of a parallelogram.
Answer: ∠A =∠C = 65°; ∠B =∠D = 115°.
Task 2. The sum of two angles of a parallelogram is 220°. Find the angles of the parallelogram.
 Since a parallelogram has 2 equal acute angles and 2 equal obtuse angles, we are given the sum of two obtuse angles, i.e. ∠B +∠D = 220°. Then ∠B =∠D = 220° :
2 = 110°.
Since a parallelogram has 2 equal acute angles and 2 equal obtuse angles, we are given the sum of two obtuse angles, i.e. ∠B +∠D = 220°. Then ∠B =∠D = 220° :
2 = 110°.
∠A + ∠B = 180° as angles adjacent to one side of a parallelogram, so ∠A = 180° - ∠B = 180° - 110° = 70°. Then ∠C =∠A = 70°.
Answer: ∠A =∠C = 70°; ∠B =∠D = 110°.
Task 3. One of the angles of a parallelogram is 3 times larger than the other. Find the angles of the parallelogram.
Let ∠A =x. Then ∠B = 3x. Knowing that the sum of the angles of a parallelogram adjacent to one of its sides is 180°, we will create an equation.
x = 180 : 4;
We get: ∠A = x = 45°, and ∠B = 3x = 3 ∙ 45° = 135°.
Opposite angles of a parallelogram are equal, therefore,
∠A =∠C = 45°; ∠B =∠D = 135°.
Answer: ∠A =∠C = 45°; ∠B =∠D = 135°.
Task 4. Prove that if a quadrilateral has two parallel and equal sides, then this quadrilateral is a parallelogram.
Proof.
Let's draw the diagonal BD and consider Δ ADB and Δ CBD.
AD = BC by condition. The BD side is common. ∠1 = ∠2 as internal crosswise lying with parallel (by condition) lines AD and BC and secant BD. Therefore, Δ ADB = Δ CBD on two sides and the angle between them (1st sign of equality of triangles). In congruent triangles, the corresponding angles are equal, which means ∠3 =∠4. And these angles are internal angles lying crosswise with straight lines AB and CD and secant BD. This implies that the lines AB and CD are parallel. Thus, in this quadrilateral ABCD, the opposite sides are parallel in pairs, therefore, by definition, ABCD is a parallelogram, which is what needed to be proven.
Task 5. The two sides of a parallelogram are in the ratio 2 : 5, and the perimeter is 3.5 m. Find the sides of the parallelogram.

∙ (AB + AD).
Let's denote one part by x. then AB = 2x, AD = 5x meters. Knowing that the perimeter of the parallelogram is 3.5 m, we create the equation:
2 ∙ (2x + 5x) = 3.5;
2 ∙ 7x = 3.5;
x = 3.5 : 14;
One part is 0.25 m. Then AB = 2 ∙ 0.25 = 0.5 m; AD = 5 ∙ 0.25 = 1.25 m.
Examination.
Perimeter of parallelogram P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1.75 = 3.5 (m).
Since the opposite sides of the parallelogram are equal, then CD = AB = 0.25 m; BC = AD = 1.25 m.
Answer: CD = AB = 0.25 m; BC = AD = 1.25 m.
A parallelogram is a quadrilateral whose opposite sides are parallel in pairs.
This definition is already sufficient, since the remaining properties of the parallelogram follow from it and are proved in the form of theorems.
- The main properties of a parallelogram are:
- a parallelogram is a convex quadrilateral;
- A parallelogram has opposite sides that are equal in pairs;
- In a parallelogram, opposite angles are equal in pairs;
The diagonals of a parallelogram are divided in half by the point of intersection.
Parallelogram - convex quadrilateral Let us first prove the theorem that a parallelogram is a convex quadrilateral
. A polygon is convex if whichever side of it is extended to a straight line, all other sides of the polygon will be on the same side of this straight line.
Parallel segments have no common points and do not intersect. This means that CD lies on one side of AB. Since segment BC connects point B of segment AB with point C of segment CD, and segment AD connects other points AB and CD, segments BC and AD also lie on the same side of line AB where CD lies. Thus, all three sides - CD, BC, AD - lie on the same side of AB.
Similarly, it is proved that in relation to the other sides of the parallelogram, the other three sides lie on the same side.
Opposite sides and angles are equal
One of the properties of a parallelogram is that In a parallelogram, opposite sides and opposite angles are equal in pairs. For example, if a parallelogram ABCD is given, then it has AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. This theorem is proven as follows.
A parallelogram is a quadrilateral. This means it has two diagonals. Since a parallelogram is a convex quadrilateral, any of them divides it into two triangles. In the parallelogram ABCD, consider the triangles ABC and ADC obtained by drawing the diagonal AC.
These triangles have one side in common - AC. Angle BCA is equal to angle CAD, as are vertical when BC and AD are parallel. Angles BAC and ACD are also equal to vertical angles when AB and CD are parallel. Therefore, ∆ABC = ∆ADC at two angles and the side between them.
In these triangles, side AB corresponds to side CD, and side BC corresponds to AD. Therefore, AB = CD and BC = AD.
Angle B corresponds to angle D, i.e. ∠B = ∠D. Angle A of a parallelogram is the sum of two angles - ∠BAC and ∠CAD. Angle C is equal to ∠BCA and ∠ACD. Since pairs of angles are equal to each other, then ∠A = ∠C.
Thus, it is proven that in a parallelogram opposite sides and angles are equal.
Diagonals are divided in half
Since a parallelogram is a convex quadrilateral, it has two diagonals, and they intersect. Let parallelogram ABCD be given, its diagonals AC and BD intersect at point E. Consider the triangles ABE and CDE formed by them.

These triangles have sides AB and CD equal to the opposite sides of a parallelogram. Angle ABE is equal to angle CDE as crosswise lying with parallel lines AB and CD. For the same reason, ∠BAE = ∠DCE. This means ∆ABE = ∆CDE at two angles and the side between them.
You can also notice that angles AEB and CED are vertical and therefore also equal to each other.
Since triangles ABE and CDE are equal to each other, then all their corresponding elements are equal. Side AE of the first triangle corresponds to side CE of the second, which means AE = CE. Similarly BE = DE. Each pair of equal segments constitutes a diagonal of a parallelogram. Thus it is proven that The diagonals of a parallelogram are bisected by their intersection point.
A parallelogram is a quadrilateral whose opposite sides are parallel, i.e. lie on parallel lines
Properties of a parallelogram: 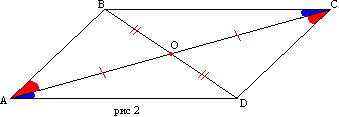 Theorem 22.
Opposite sides of a parallelogram are equal.
Theorem 22.
Opposite sides of a parallelogram are equal.
Proof. In the parallelogram ABCD we draw a diagonal AC. Triangles ACD and ACB are equal, as if they have common side AC and two pairs of equal angles. adjacent to it: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (as crosswise angles with parallel lines AD and BC). This means that AB = CD and BC = AD, as the corresponding sides of equal triangles, etc. From the equality of these triangles it also follows that the corresponding angles of the triangles are equal:
Theorem 23.
The opposite angles of the parallelogram are equal: ∠ A=∠ C and ∠ B=∠ D.
The equality of the first pair comes from the equality of triangles ABD and CBD, and the second - ABC and ACD.
Theorem 24.
Adjacent angles of a parallelogram, i.e. angles adjacent to one side add up to 180 degrees.
This is so because they are interior one-sided angles.
Theorem 25.
The diagonals of a parallelogram bisect each other at their intersection point.
Proof. Consider triangles BOC and AOD. According to the first property, AD=BC ∠ OAD=∠ OCB and ∠ ODA=∠ OBC lying crosswise for parallel lines AD and BC. Therefore, triangles BOC and AOD are equal in side and adjacent angles. This means BO=OD and AO=OS, like the corresponding sides of equal triangles, etc.
Signs of a parallelogram
Theorem 26.
If the opposite sides of a quadrilateral are equal in pairs, then it is a parallelogram.
Proof. Let the quadrilateral ABCD have sides AD and BC, AB and CD respectively equal (Fig. 2). Let's draw the diagonal AC. Triangles ABC and ACD are equal on three sides. Then angles BAC and DCA are equal and, therefore, AB is parallel to CD. The parallelism of sides BC and AD follows from the equality of angles CAD and ACB.
Theorem 27.
If the opposite angles of a quadrilateral are equal in pairs, then it is a parallelogram.
Let ∠ A=∠ C and ∠ B=∠ D. Because ∠ A+∠ B+∠ C+∠ D=360 o, then ∠ A+∠ B=180 o and sides AD and BC are parallel (based on the parallelism of straight lines). We will also prove the parallelism of sides AB and CD and conclude that ABCD is a parallelogram by definition.
Theorem 28.
If adjacent corners of a quadrilateral, i.e. The angles adjacent to one side add up to 180 degrees, then it is a parallelogram.
If the internal one-sided angles add up to 180 degrees, then the straight lines are parallel. So AB is parallel to CD and BC is parallel to AD. A quadrilateral turns out to be a parallelogram by definition.
Theorem 29.
If the diagonals of a quadrilateral bisect each other at the point of intersection, then the quadrilateral is a parallelogram.
Proof. If AO = OC, BO = OD, then triangles AOD and BOC are equal, as having equal (vertical) angles at vertex O, enclosed between pairs of equal sides. From the equality of triangles we conclude that AD and BC are equal. The sides AB and CD are also equal, and the quadrilateral turns out to be a parallelogram according to criterion 1.
Theorem 30.
If a quadrilateral has a pair of equal, parallel sides, then it is a parallelogram.
Let the sides AB and CD of quadrilateral ABCD be parallel and equal. Let's draw diagonals AC and BD. From the parallelism of these lines it follows that the crosswise angles ABO = CDO and BAO = OCD are equal. Triangles ABO and CDO are equal in side and adjacent angles. Therefore AO=OS, VO=ОD, i.e. The diagonals are divided in half by the intersection point and the quadrilateral turns out to be a parallelogram according to criterion 4.
In geometry, special cases of parallelograms are considered.




